Продолжаются совместные научные исследования с Республикой Узбекистан

   В рамках подписанного ранее соглашения о научном сотрудничестве между ИКИР ДВО РАН и Институтом математики им. В. И. Романовского (г. Ташкент, Узбекистан) продолжается работа в области математических исследований.

   В журнале Mathematics (июль 2023 г.) опубликована совместная статья научных сотрудников данных институтов "Optimization of the Approximate Integration Formula Using the Discrete Analogue of a High-Order Differential Operator", K. Shadimetov, A. Boltaev, R. Parovik ("Оптимизация формулы приближенного интегрирования с использованием дискретного аналога дифференциального оператора высокого порядка", авторы Х. М. Шадиметов, А. К. Болтаев, Р. И. Паровик) // Mathematics, 2023, 11(14), 3114; https://doi.org/10.3390/math11143114.

   Известно, что дискретные аналоги дифференциальных операторов играют важную роль при построении оптимальных квадратурных, кубатурных и разностных формул. Используя дискретные аналоги дифференциальных операторов, можно построить оптимальные интерполяционные, квадратурные и разностные формулы, точные для алгебраических многочленов, тригонометрических и экспоненциальных функций. В этой статье мы строим дискретный аналог ^_Dm(hβ) дифференциального оператора 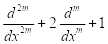 в гильбертовом пространстве 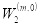. Разработан алгоритм построения оптимальных квадратурных формул, точных на показательно-тригонометрических функциях, с использованием дискретного оператора. На основе этого алгоритма при m = 2 мы даем оптимальную квадратурную формулу, точную для тригонометрических функций. Наконец, приведем скорость сходимости оптимальной квадратурной формулы в гильбертовом пространстве 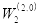для случая m = 2.

   Ознакомиться с полным текстом статьи можно по ссылке.