Научный сотрудник ИКИР ДВО РАН, к.ф.-м.н., Твёрдый Д. А. выступил на Международной научно-практической конференции «Актуальные вопросы алгебры и анализа» в г. Термез, Республика Узбекистан

Цель конференции: Расширение сотрудничества учёных, работающих в системе международных и республиканских вузов, а также в научно-исследовательских институтах; обсуждение новых результатов, полученных в области математики и методики её преподавания, а также определение перспективных направлений развития математики.

Конференция была организована Министерством высшего образования, науки и инноваций Республики Узбекистан, Термeзским государственным университетом, Академией наук Республики Узбекистан, Институтом математики им. В. И. Романовского.

Дмитрий Александрович представил доклад на тему: "Анализ эффективности и сложности параллельных алгоритмов численного решения в модели объёмной активности радона с дробной производной переменного порядка", авторы: Д. А. Твёрдый, Р. И. Паровик.

В современной науке уделяют пристальное внимание фундаментальным направлениям, имеющим практическое применение. Для Камчатского края, в частности, это исследование процессов миграции подпочвенного газа радона с помощью наиболее современных методов математического моделирования с целью интерпретации аномалий, предшествующих землетрясениям.

В приведённом исследовании рассматриваются параллельные реализации численных методов решения: нелокальных EFDS и IFDS-MNM с целью оценок вычислительной сложности и эффективности данных алгоритмов. Данные алгоритмы реализуют решения прямых задач математического моделирования на основе ранее предложенных авторами эредитарных моделях объемной активности радона (ОАР) с учётом нелокальности процесса переноса радона по времени. Также для данных моделей возможна постановка обратных задач, в ходе решения которых возникает необходимость в циклическом пересчете прямой задачи при разных значениях параметров моделей и сопоставлении результатов с экспериментальными данными.

При этом прямая задача может иметь достаточно высокую вычислительную сложность как при увеличении размера входных данных N, так и при выборе метода решения. Поэтому важно, чтобы решение каждой отдельной прямой задачи выполнялось за наименьшее время, но при этом необходимо учитывать возможные затраты по памяти используемого алгоритма. Всё это приводит нас к разработке, анализу и оценкам различных параллельных алгоритмов численного решения модельных уравнений ОАР.

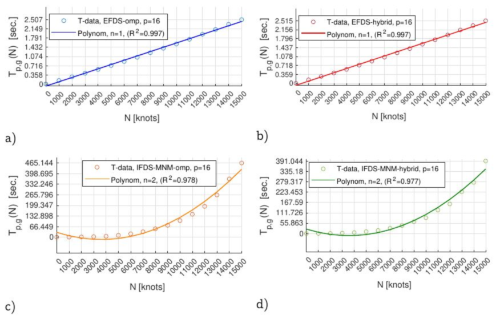
В результате показано, что параллельные алгоритмы EFDS-omp и EFDS-hybrid не дают существенного прироста в скорости вычислений (порядка 30%) по сравнению с EFDS. В то же время, параллельные алгоритмы IFDS-MNM-omp и IFDS-MNM-hybrid дают серьёзный прирост в ускорении вычислений в 13 и 17 раз соответственно, при увеличении затрат RAM не более чем в 2.5 и 5 раз соответственно, по сравнению с последовательным IFDS-MNM; Параллельные алгоритмы EFDS-omp и EFDS-hybrid имеют асимптотически точную оценку сложности по времени порядка (n), однако по RAM оценка уже порядка (n2); Алгоритмы IFDS-MNM-omp и IFDS-MNM-hybrid имеют асимптотически точные оценки сложности по времени и RAM порядка (n2).